MEV Agents: Optimizing DeFi Trades
In decentralized finance (DeFi), Maximum Extractable Value (MEV) agents have emerged as a crucial tool for traders looking to optimize their execution. These agents actively analyze real-time transaction data, detecting peer-to-peer matches and profitable ring trades that unlock the best prices for trades or limit orders. By considering factors like liquidity, order book depth, and price slippage, MEV agents ensure that traders achieve the most efficient execution possible.
Whether interacting directly with on-chain automated market makers (AMMs) or leveraging decentralized exchange (DEX) aggregators, MEV agents continuously assess and route transactions through the most advantageous paths, making them an integral part of modern DeFi ecosystems.
In this post, I'll guide youu thorugh the development of a MEV agent that can match a set of order intents (in JSON) to various potential liquidity sources and determine the optimal execution to maximize the order's surplus.
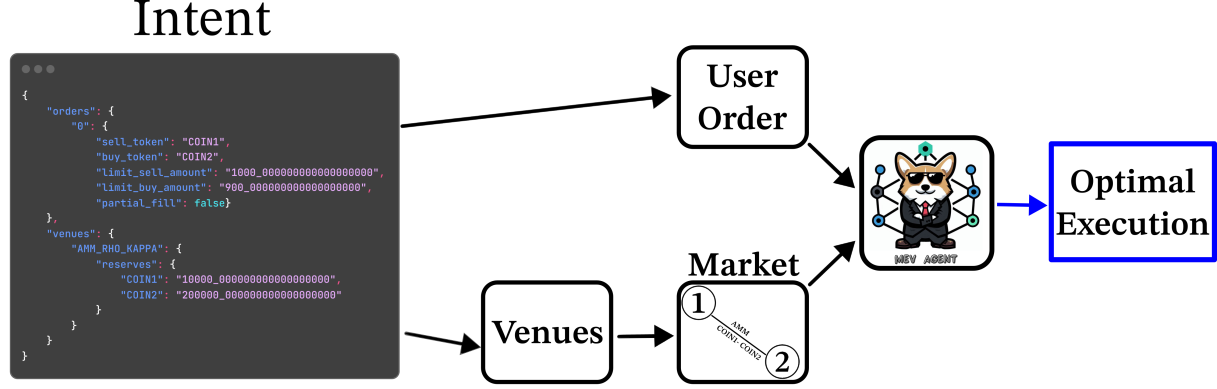
For instance, here is a simple example of an order intent:
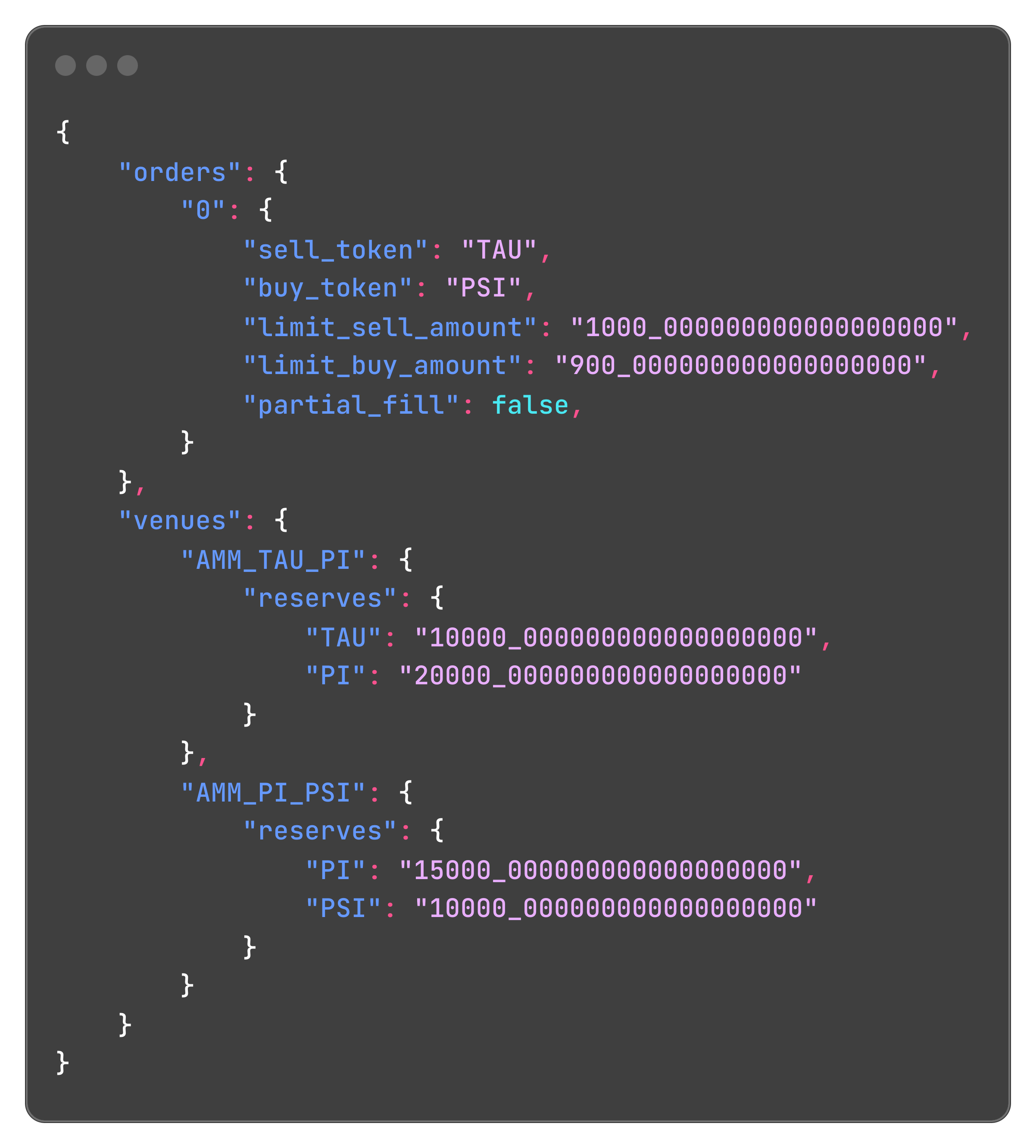
Setting the Framework
Suppose a user with an order expressing their intent to buy buy_token and sell sell_token with specified restrictions. These restrictions include the maximum amount of sell_token the user is willing to sell (s_lim) and the minimum amount of buy_token the user is willing to receive (b_lim).
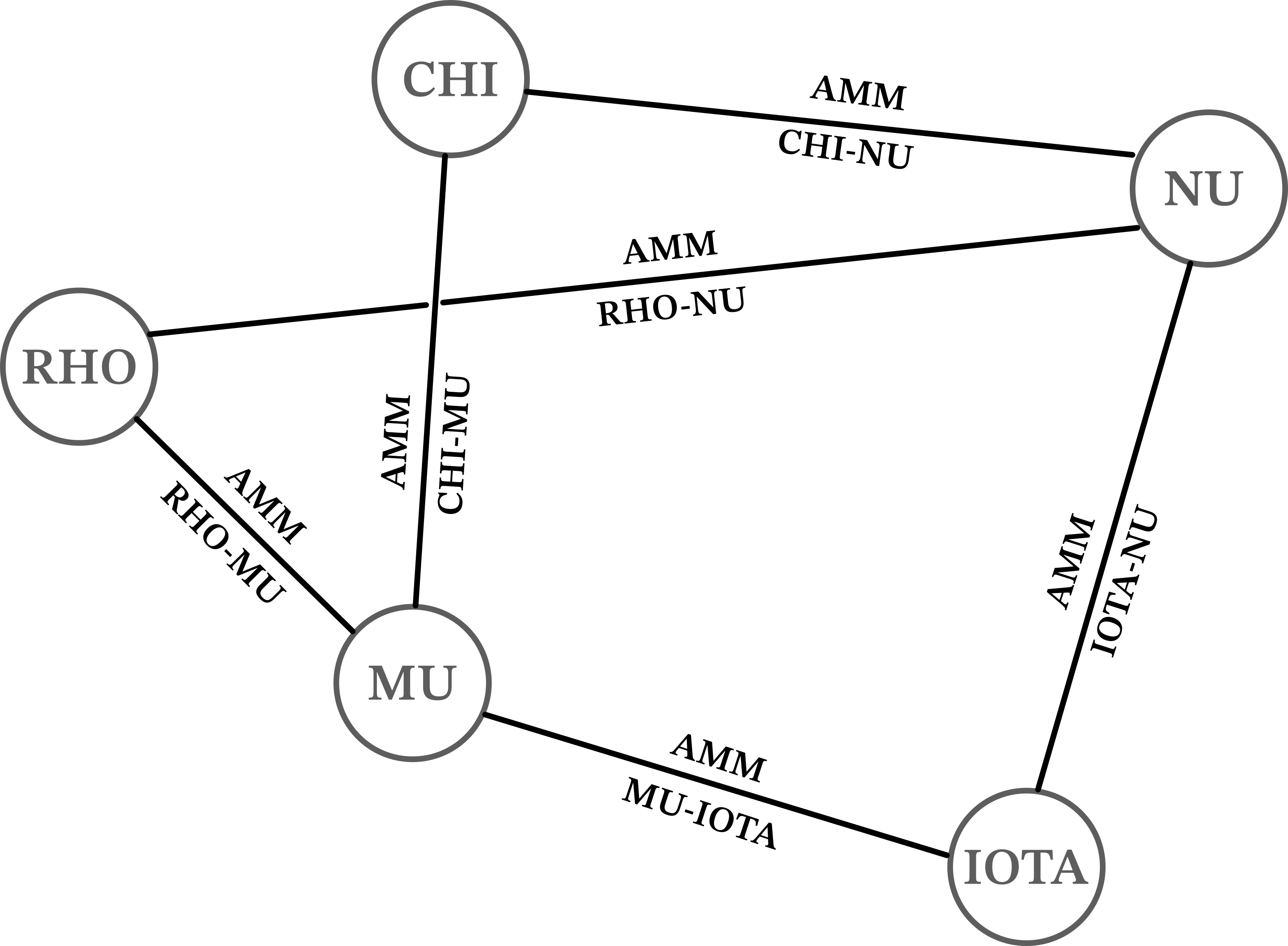
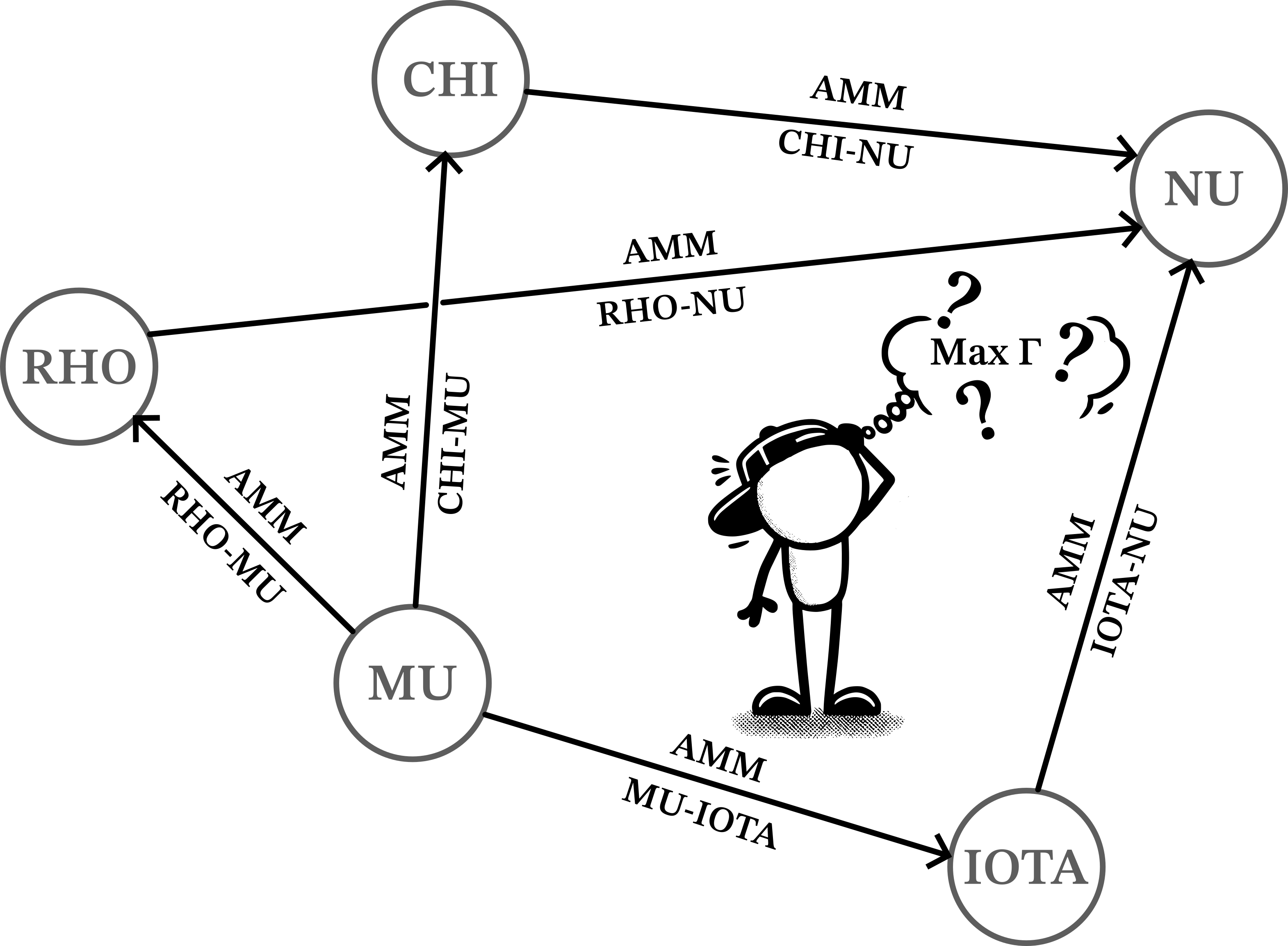
We have a set of venues or liquidity pools with an AMM where coins can be swapped. All the coins and venues define an undirected graph, with the former being the vertices and the latter being the edges. For example:
The order's surplus Γ is defined as:
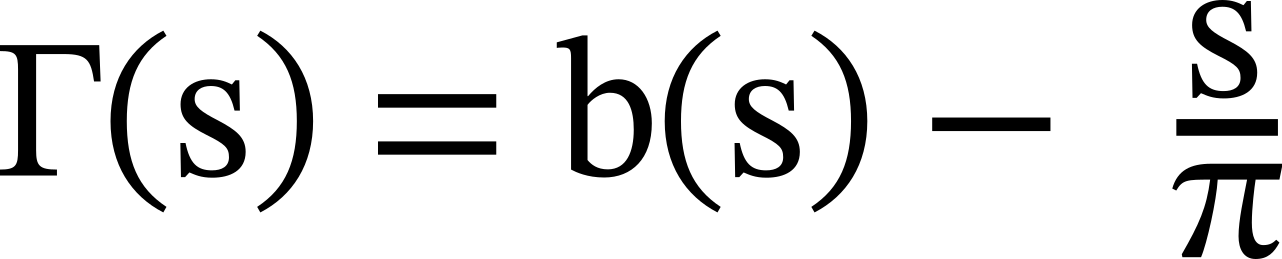
Where π = s_lim / b_lim is the user's worst acceptable exchange rate.
The problem posed is: if users has 1000 MU (sell_token), what is the optimal way to convert it into NU (buy_token)? These problems are called forward routing.
Interestingly, for such problems, direct routes (i.e., selling all 1000 MU along a single simple path connecting MU to NU), are not always the most efficient, and a combination of multiple routes can often yield better results.
Thus, the task translates into helping the user solve this problem:
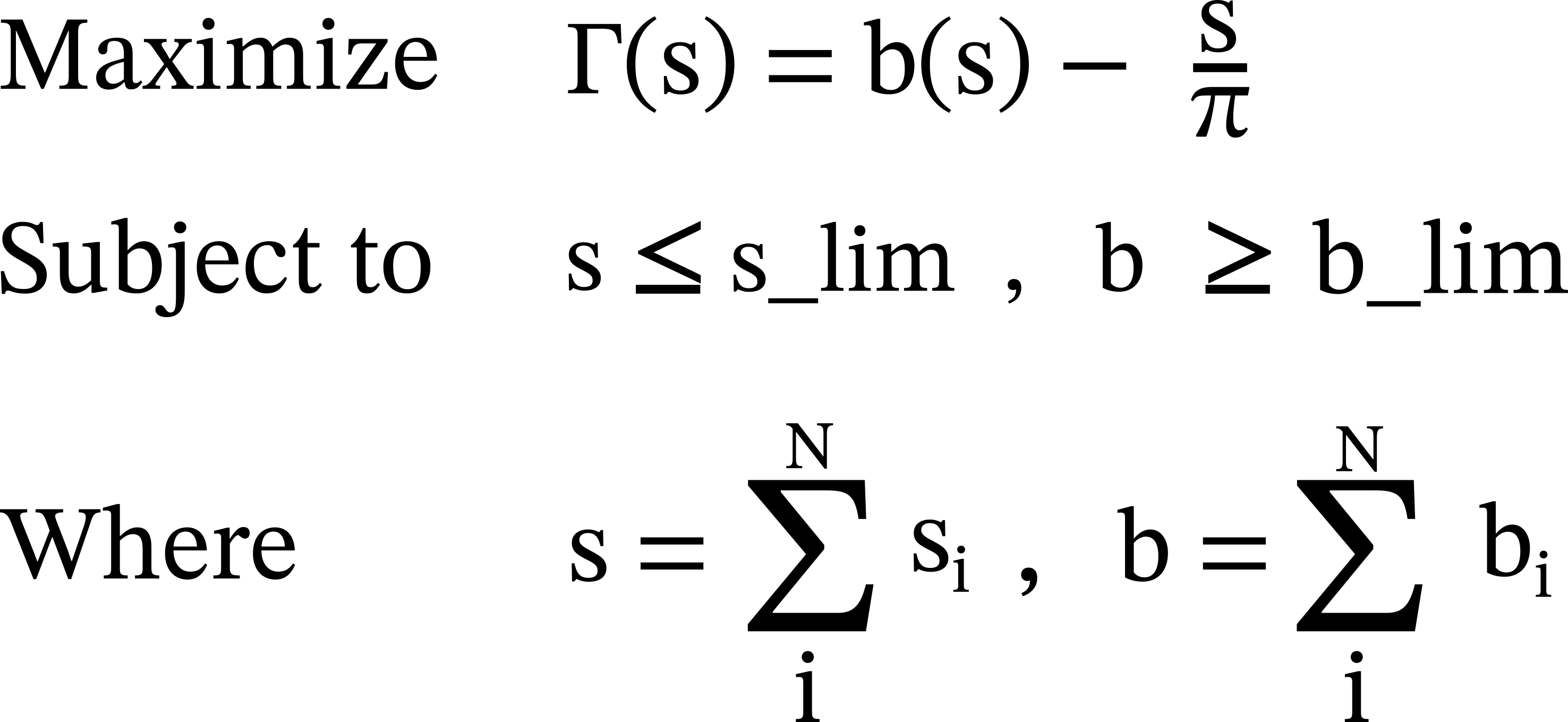
With N being the number of simple paths connecting sell_token with buy_token (MU and NU in our example, respectively).
Gladly, the forward routing problem is convex, so we do not have to embark on a global optimization problem but can employ local minimizers.
My Approach
There are many ways to solve this problem. In my solution, the main components are a set of classes:
Order: Represents an order with user intent for trading.Venue: Represents a trading venue with token reserves.Market: Represents a market of trading venues; it is a graph with tokens at the vertices and venues at the edges.Agent: Represents a market agent that formulates and optimizes trading strategies.
Given a generic intent, with the user Order and the list of Venues forming a Market graph, Agent reads the Market and constructs a strategy to fulfill the user's swap needs.
In this case, strategy is a directed subgraph of Market containing all the simple paths connecting the user requested sell_token to buy_token.
The Agent now searches for the optimal coin exchange among the paths in the strategy to maximize the user surplus by applying a constrained maximization of the order's surplus Γ function defined above.
This is the scheme of such an approach:
Which translates into this code:

One can call such function with a simple Python program:
That when is run for the previous intent outputs:
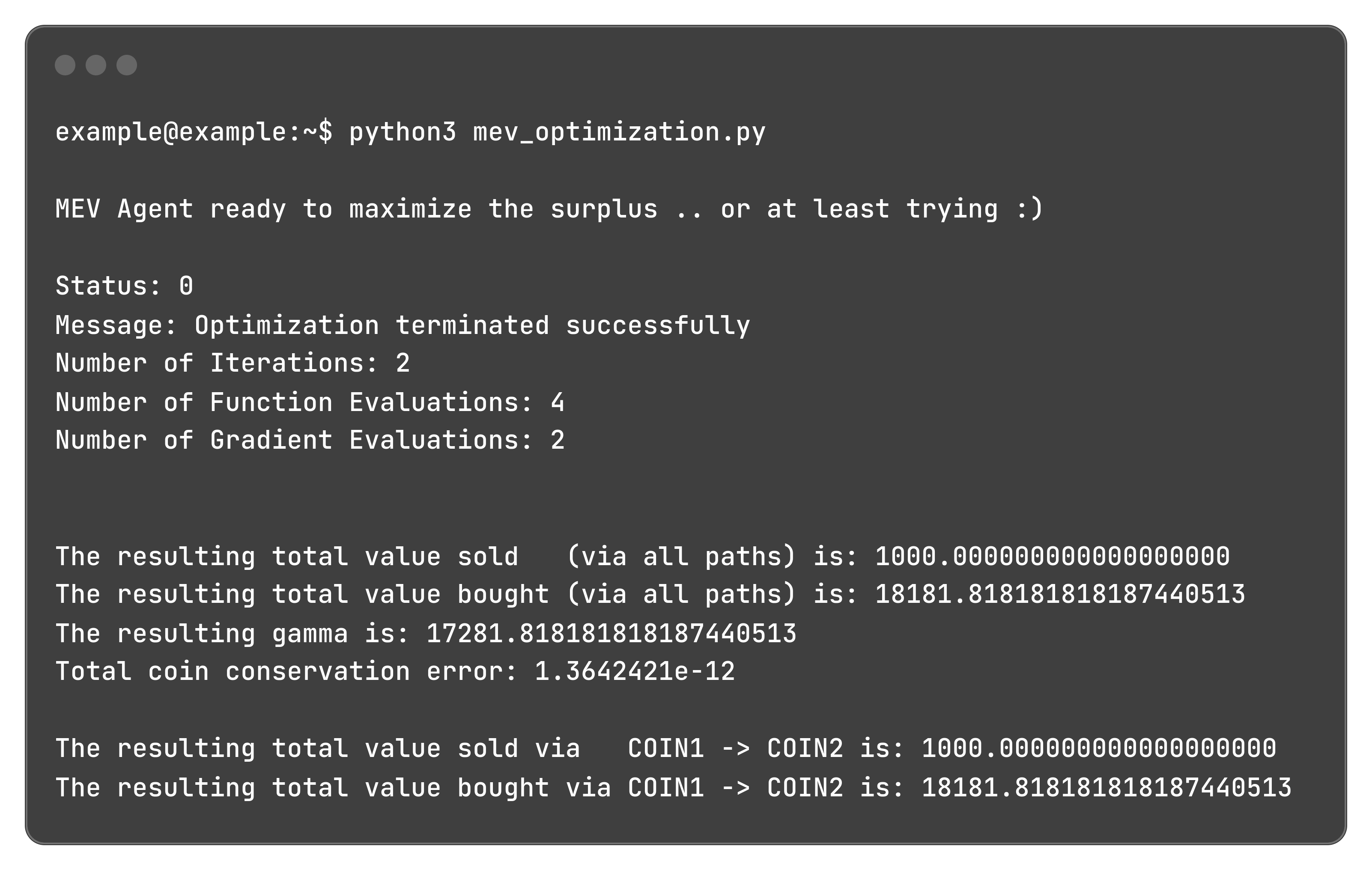
Generating the following results:

That's enough to make it work.
However, If you want more technical details on how such code works, sit down and fasten your belt.
Technical Discussion
In this first steps, we build:
- The user
Ordercontaining the intent of buyingbuy_tokenand sellingsell_token, with the worst acceptable exchange rate; - The
Venueobjects containing the trading venues; - The
Marketobject, i.e., the graph of coins and trading venues.
The User Order's
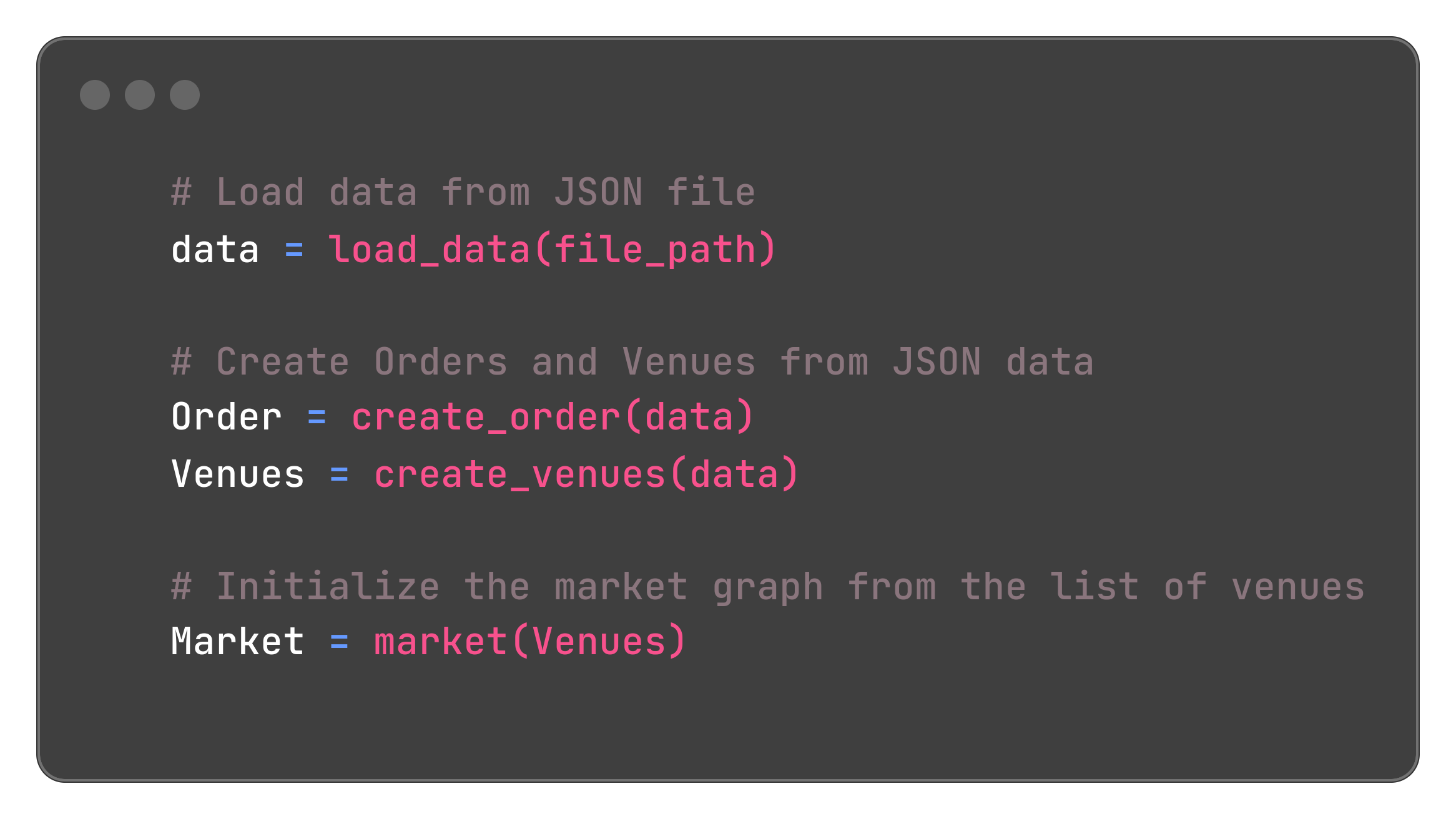
First of all, we ingest the intent into the variable data and read values from it:
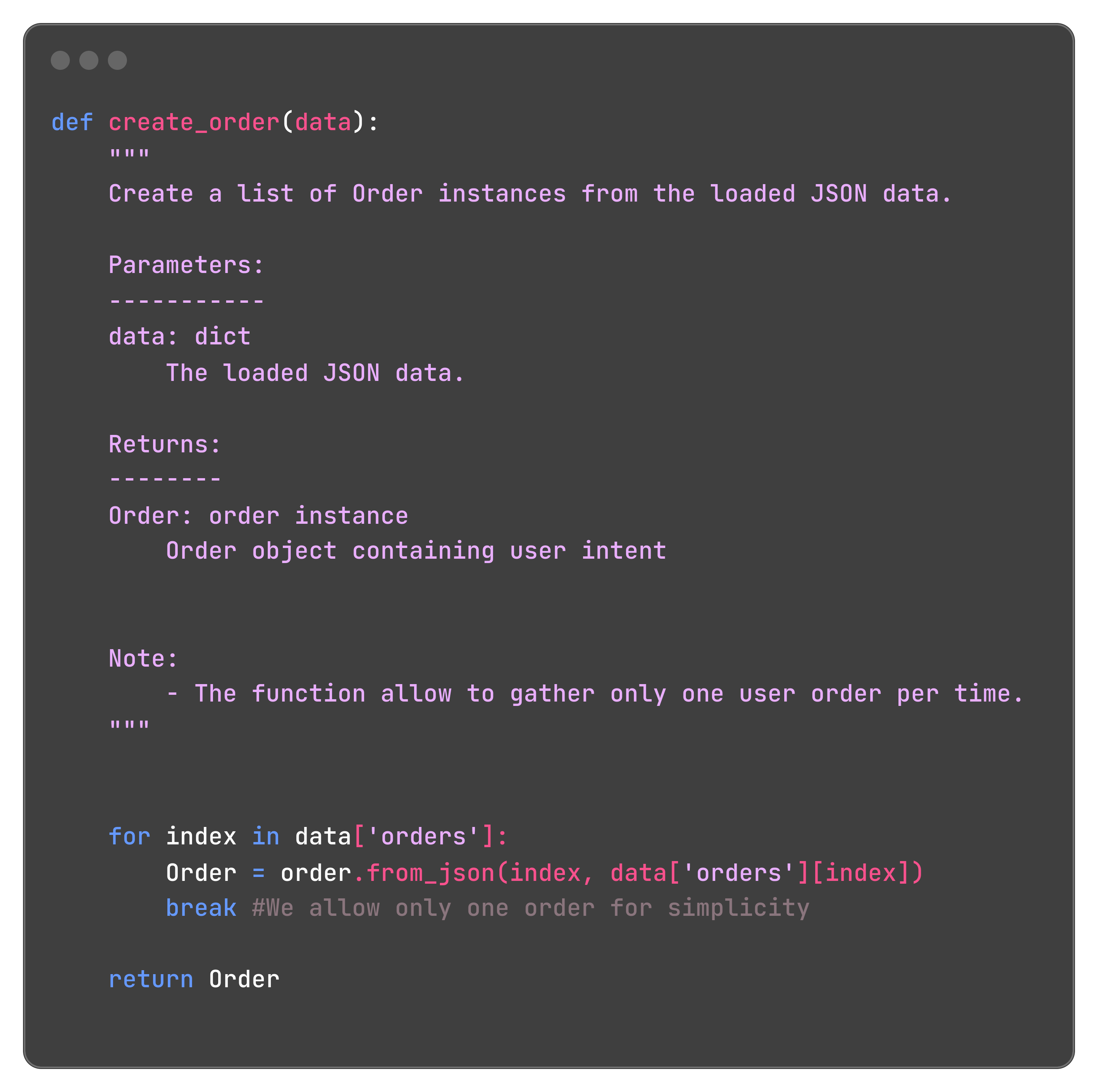
This allows to initialize an instance of the class order:
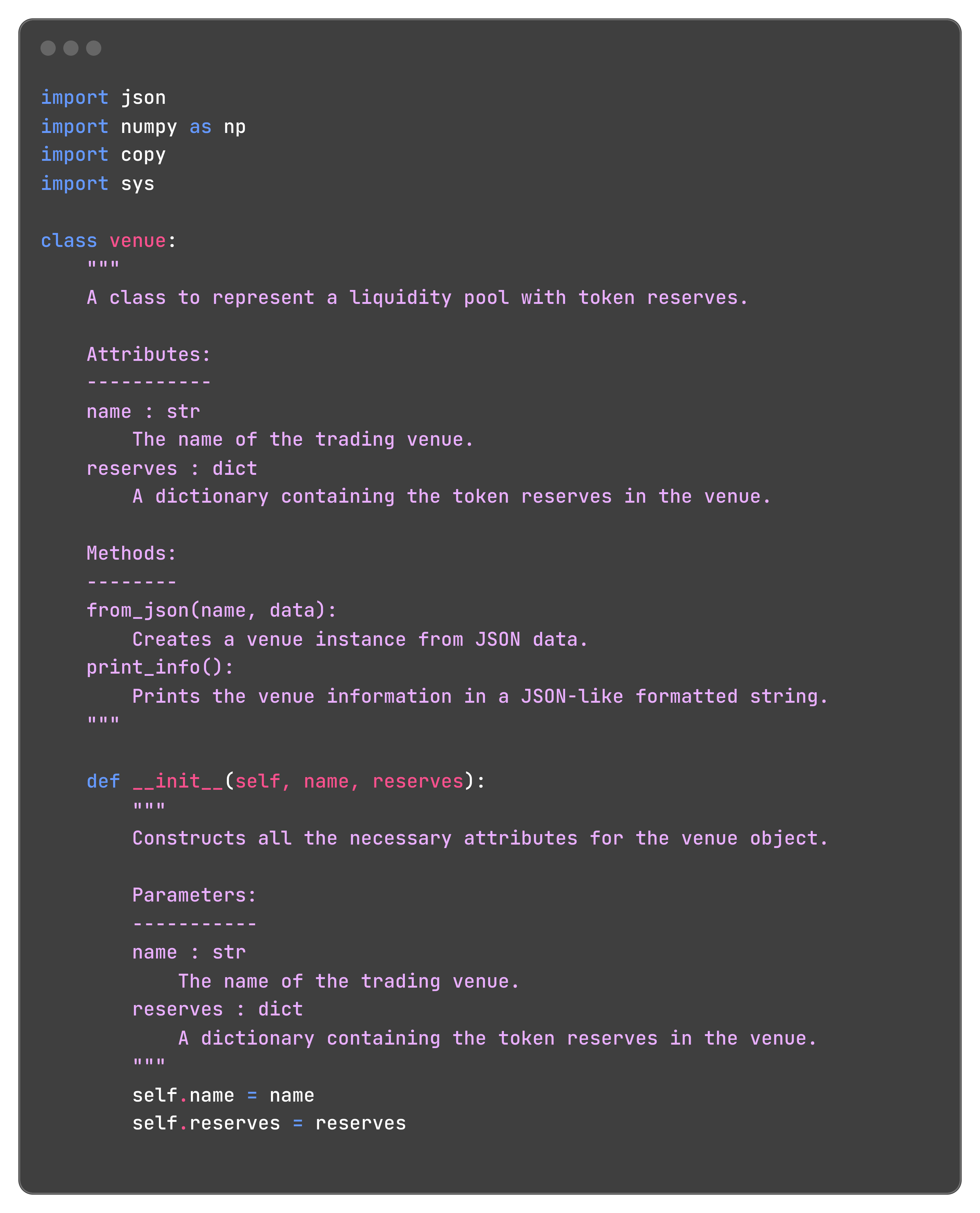
The Venues
Next, we include all the venues:
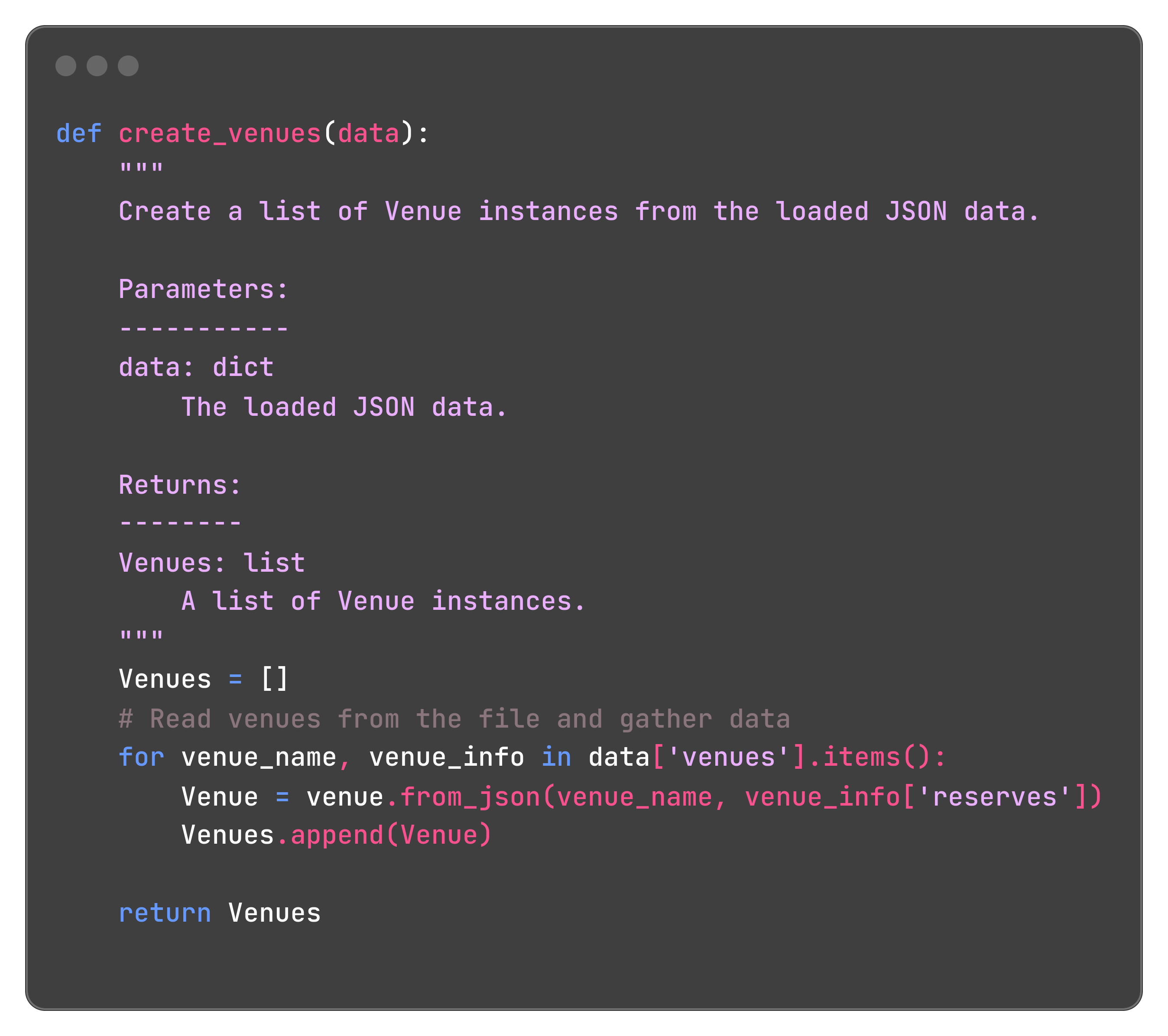
This allows to initialize a list of instances of the class venue:
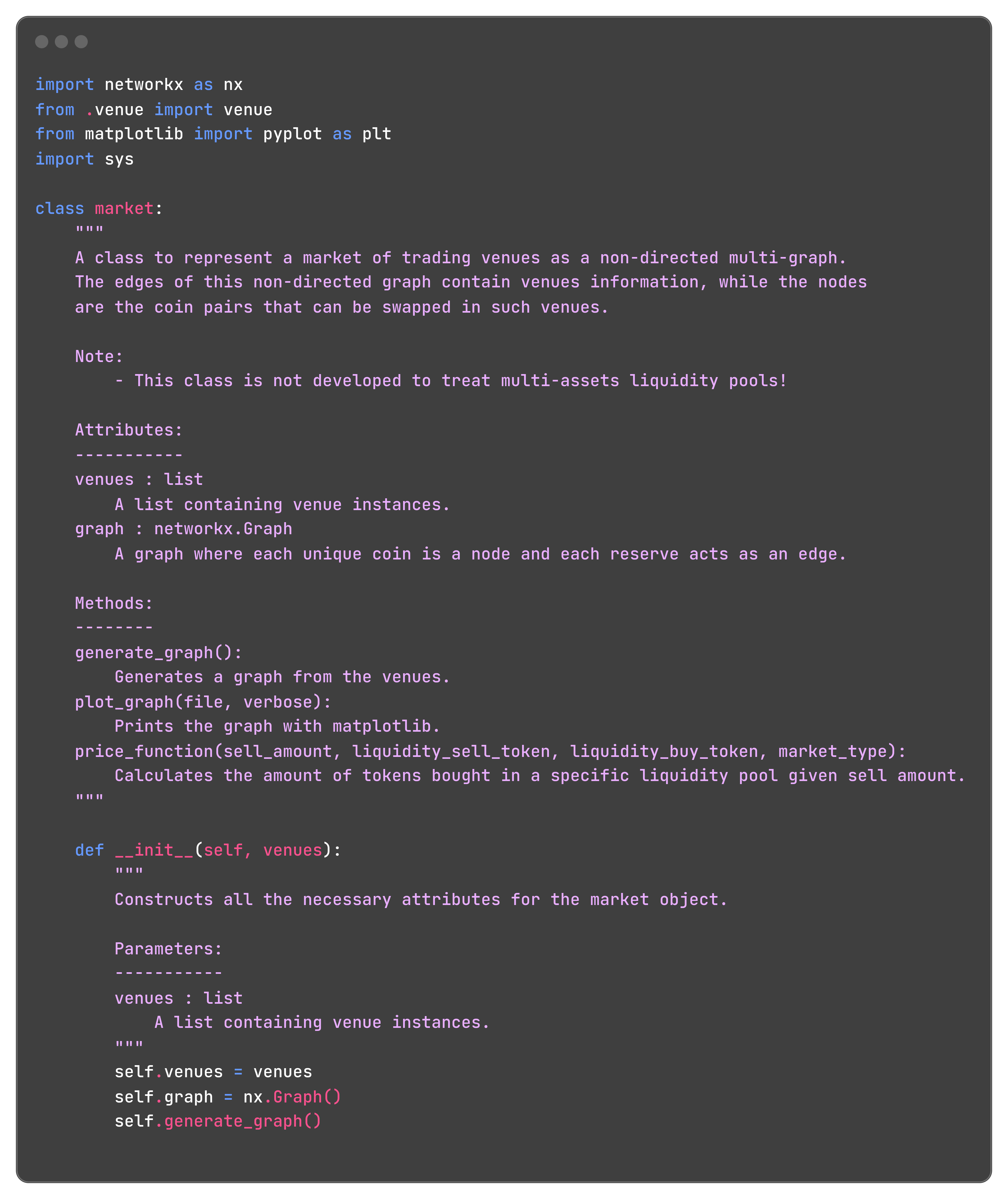
The Market
Having stored the venues, we can now build the Market graph:
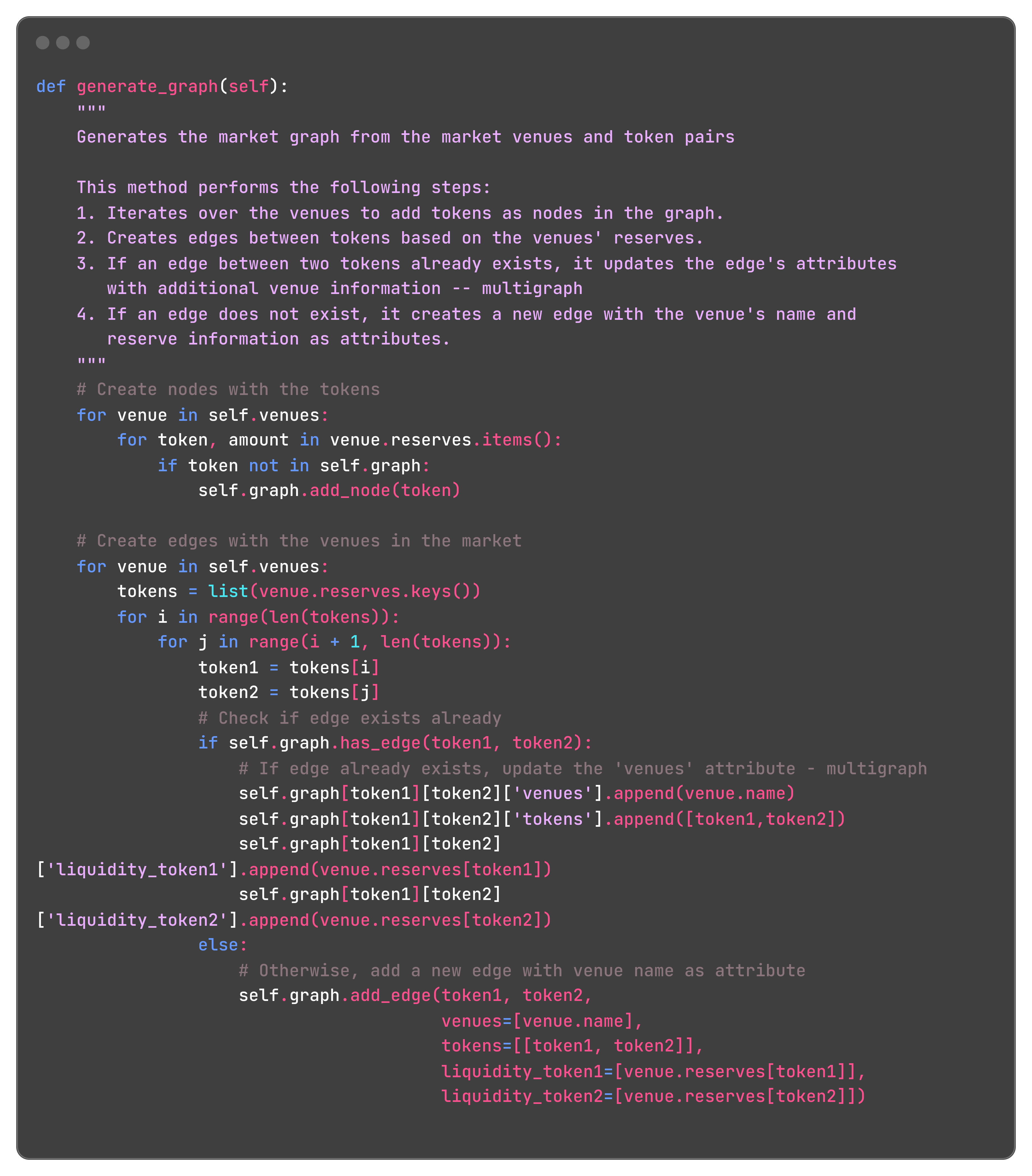
The initialization of a market instance generates the graph as follows:
In our example, Market will look something like:
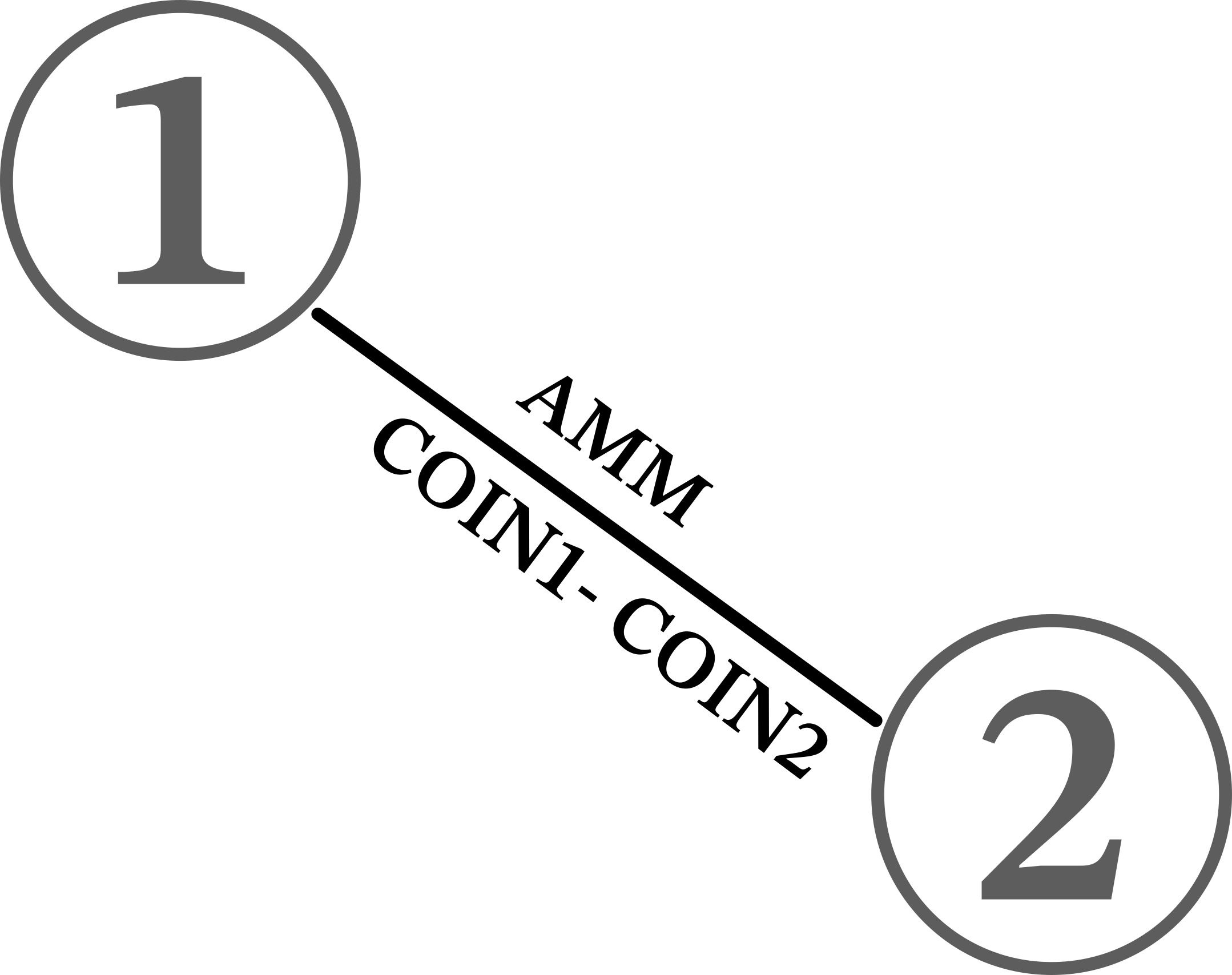
The Agent
Now, that we have all the necessary inputs, we can initialize the Agent and construct the strategy graph:

Where the Agent object looks like:
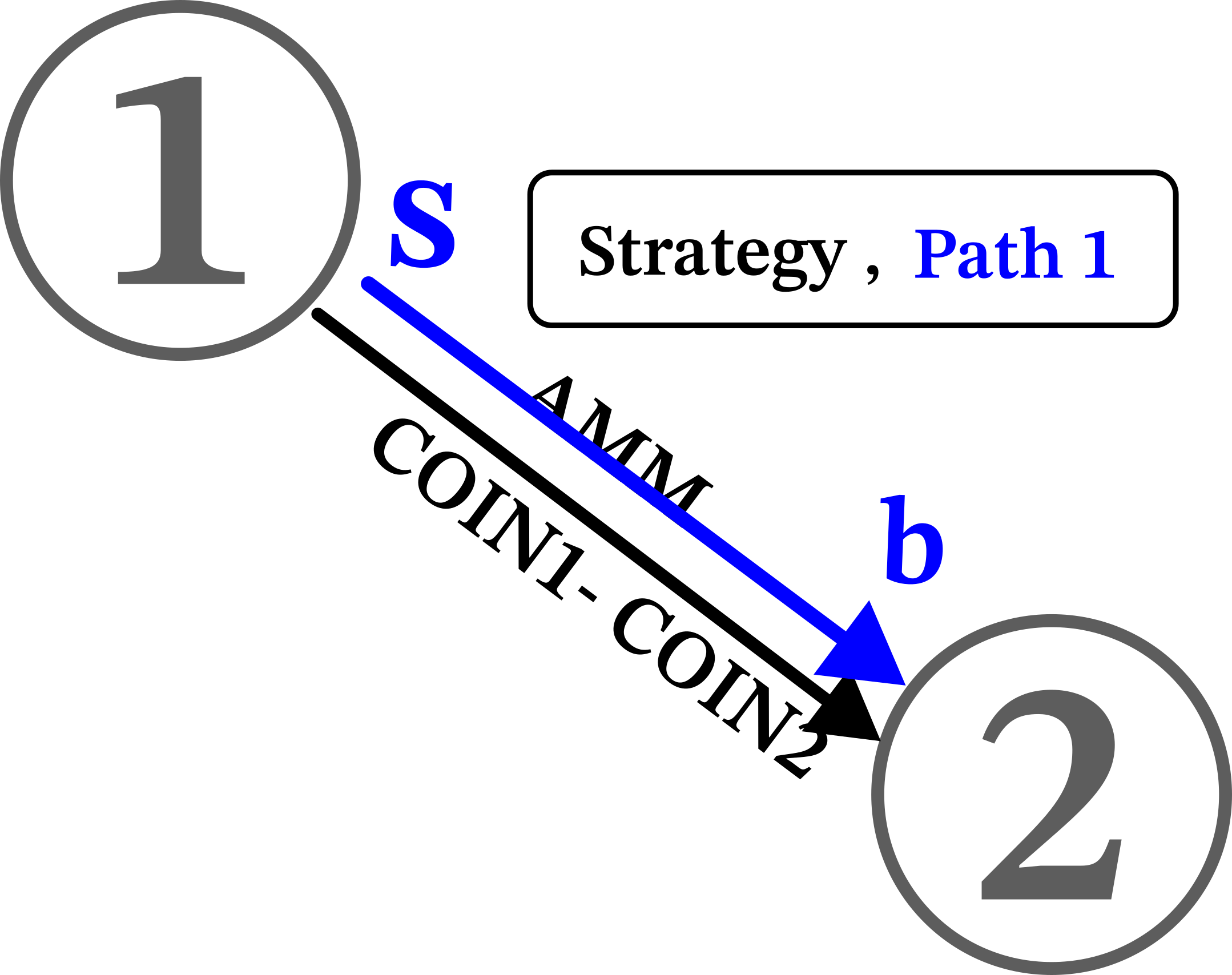
Strategy Construction
Strategy is a directed subgraph of Market. Agent, stores also all the paths connecting sell_token to buy_token. In our case, this will look something like:
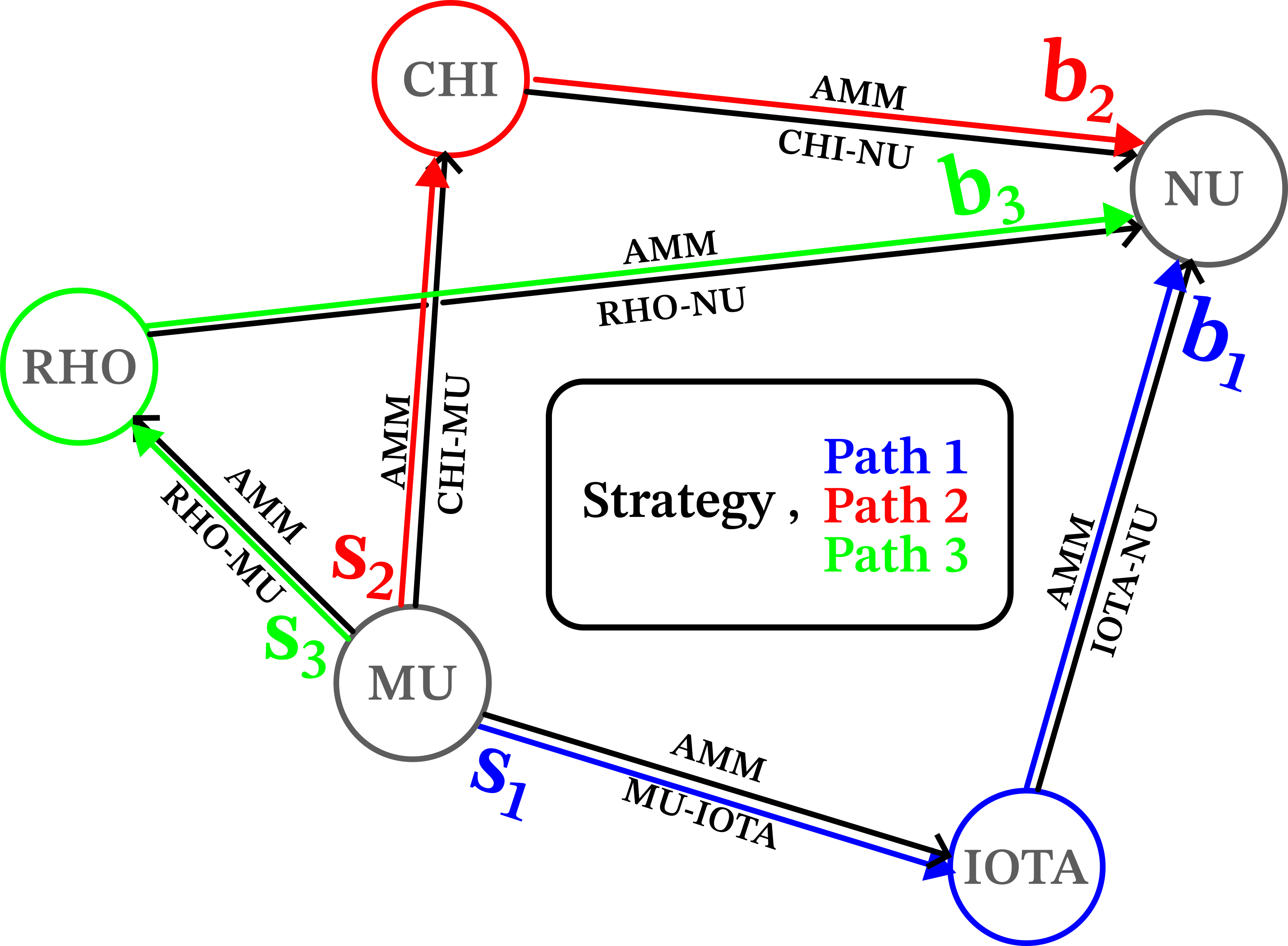
In case of more complex graphs, multiple paths are stored for future propagation and optimization, for example:
To do this, we first read the Market with the method:
And then, we construct the strategy multigraph:
The Strategy Optimization
Now we have all the ingredients to try to solve our forward routing problem:
- We have the intents of the user defining the constraint of our problem;
- We have the paths along which we can propagate to reach
buy_tokenfromsell_token; - Having set the direction of propagation, we also have the price function for each edge, allowing swapping from one coin to another through an AMM venue.
Note: the price function of the venue AMM C-A will be in an AMM:
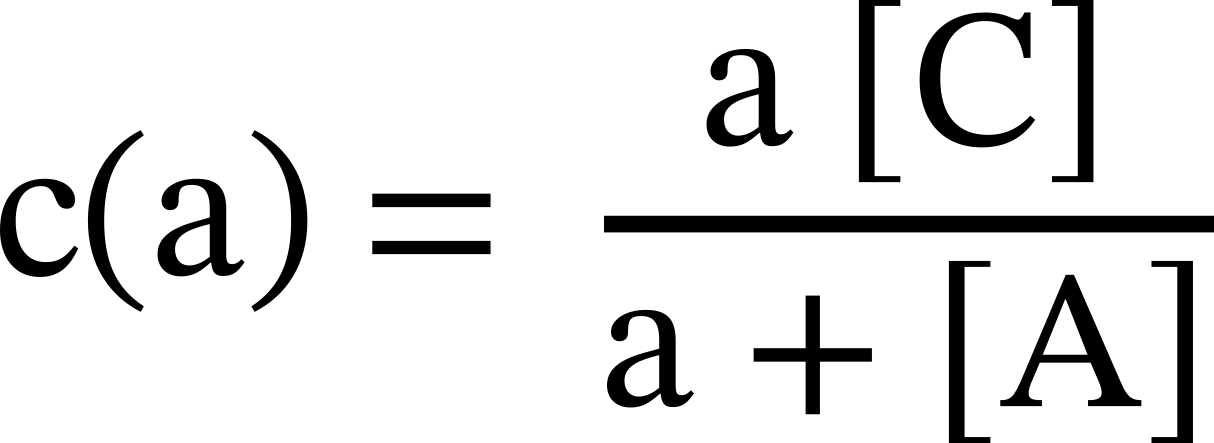
Where a is the amount of coin A sold to buy the amount c of coin C. [A], [C] are the initial liquidities of the tokens.
Now we can use the optimize_strategy method bound to Agent:
In this routine, we make use of the propagate along (path) which is defined as:
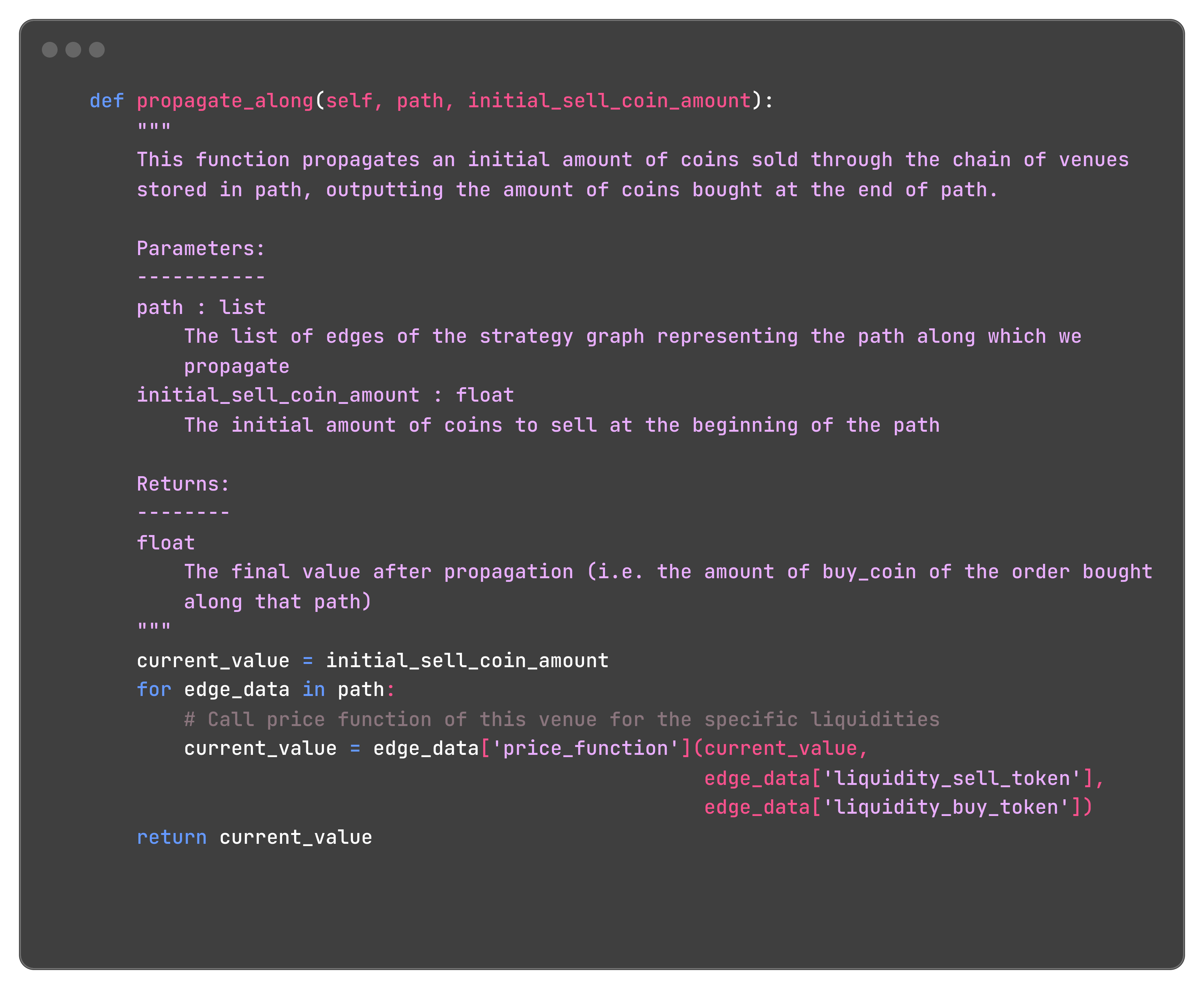
And that's all.
Now we have obtained the optimal amount of coins sold and bought through each channel, we just need to output the results to the user.
Final Thoughts
The approach I employed works on acyclic graphs. Adding an edge between two coins makes the graph become a multigraph. From a theoretical point of view, the problem of routing on multigraphs is still convex (e.g., see this reference).
The code works fine for very simple multigraphs (i.e., only two coins are connected by more than one venue).
However, when multiple venues connect multiple coins, the problem of detecting all simple paths connecting sell_token to buy_token arises. This problem is combinatorial by nature and gets extremely complex as the graph's dimensions increase.
In addition to this, even if the directed graph wouldn't have multi-edged connected vertices, the problem of simple path detection from A to B is highly complex (#P-complete), and requires complex numerical techniques to be solved efficiently.
Moreover, I never considered multi-asset venues, which would imply more complex graphs and for which the price functions could change during propagation. Indeed, if I consider a multi-asset pool, with tokens A, B, and C, it can happen that the price function c(a) might change if I first visited this venue but along a different edge of the graph (e.g., A/B).
Another source of additional complexity is the possibility that the graph changes through time. Indeed, it might be possible for new venues to be added to the market, introducing new connections among the nodes.
Eventually, I did not consider that in real swaps, liquidity pool providers' fees, venues' price functions, and price slippage, among other factors, might influence the executed outcome.
Until Next Time, Anon
The real world is much more complex than this challenge, but this was a fun start. By the way, if you like what you learned today, you can try it yourself: here is the repository for my project.
See you soon...
